专业高效
微纳加工公司

我们展示了一种低损耗集成电光马赫-曾德调制器，采用薄膜钽酸锂材料，在737 nm波长下工作，具有低的半波电压-长度积（0.65 V·cm）、30 dB的消光比、5.3 dB的低光学损耗和20 GHz的探测器限制带宽。在环境条件下，使用4.3 dBm的芯片上功率测得相对于四分之一偏置的小于2 dB的直流偏置漂移，持续16分钟，优于使用同类薄膜锂铌酸调制器测得的8 dB。最后，使用制造的环形谐振器，在638 nm波长下估算出薄膜钽酸锂波导的光学损耗系数为0.5 dB/cm。

#离子注入铒代工

#6寸DUV步进式光刻代工，最小线宽180nm，超高性价比，可以只曝光

#提供8寸 8umSiO2热氧片

室温低损伤@GCIB抛光代工@束斑小（4-5mm）更均匀

#降低硬质材料化合物晶圆等绝大多数材料的表面粗糙度，比如金刚石 ，磷化铟，砷化镓，碳化硅

#提高复合衬底和镀膜膜层的器件层膜厚均匀性，

比如SOI LNOI  LTOI SICOI 等 SMARTCUT得到的薄膜 

或者镀膜所得到的膜层 ，比如镀了一层氮化硅，但是由于是cvd镀膜所得到的，表面的膜厚精度很差，粗糙度很差，可以通过粗糙度初步降低粗糙度，然后通过GCIB团簇离子束抛光来修整整面的膜厚均匀性 到0.5%以下举例：

未经过Trimming 工艺的 6寸LN/LTOI晶圆 数据：

Range:100-200A

经过Trimming 工艺的 6寸LN/LTOI晶圆 数据：

Range:60A以内

ALOOI晶圆；--氧化铝薄膜晶圆，键合工艺和镀膜工艺

TAOOI晶圆--氧化钽薄膜晶圆，镀膜工艺

SINOI晶圆；--超低损耗氮化硅薄膜晶圆，

SICOI晶圆；新型量子光学平台

6寸LTOI晶圆批量供应；铌酸锂的有力的竞争对手，薄膜钽酸锂晶圆

8寸LNOI晶圆;8寸LNOI助力更大规模薄膜铌酸锂产品量产

LN/LT-SOI/Si/SIN  W2W&D2W异质集成

流片： 6寸 氮化硅 铌酸锂 硅光 超高性价比流片， 1个BLOCK的价格买一整片晶圆

划重点--全国产-超高性价比-6 寸硅光-氮化硅-铌酸锂流片白皮书

我们为客户提供晶圆（硅晶圆，玻璃晶圆，SOI晶圆，GaAs，蓝宝石，碳化硅（导电，非绝缘），Ga2O3,金刚石，GaN（外延片/衬底）），镀膜（PVD,cvd,Ald，PLD）和材料（Au Cu Ag Pt Al Cr Ti Ni Sio2 Tio2 Ti3O5，Ta2O5,ZrO2,TiN，ALN,ZnO,HfO2。。更多材料），键合（石英石英键合，蓝宝石蓝宝石键合）光刻，高精度掩模版，外延，掺杂,电子束光刻等产品及加工服务(请找小编领取我们晶圆标品库存列表，为您的科学实验加速。

请联系小编免费获取原文

I. 引言
薄膜锂铌酸（TFLN）电光（EO）集成电路在推动光学科学和技术方面表现出了潜力1–5。其优势源于锂铌酸（LN）宽波长范围内较大的Pockels系数（约30 pm/V）（LN的带隙为3.63 eV），以及利用常规纳米制造技术（光刻、刻蚀等）实现低损耗光波导的能力。最近，薄膜钽酸锂（TFLT）已经商业化，并被用于电光电路，特别是在通信波长范围内6–13。这一研究主要受到钽酸锂（LT）相较于锂铌酸（LN）具有的相似或更优性能的驱动：电光系数r33~30 pm/V14，带隙为3.93 eV15，633 nm下的双折射是LN的23倍小16，近可见波长下的光折射效应是LN的5倍小17,18，绿色光的光学损伤阈值是LN的2500倍高19,20，以及RF损耗正切是LN的10倍小16,21。

较低的双折射和减少的电荷传输效应是推动TFLT光子学发展的主要因素。例如，已知光诱导的电荷传输和光伏效应会增强电光弛豫效应，这表现为由于电荷迁移导致晶体中光的光学相位的非控制性变化。特别地，随着施加的光功率增大，弛豫速率将增加，并且在施加的直流（DC）或射频（RF）场下可能会加剧这一效应。这一效应降低了电光电路的直流稳定性，如马赫-曾德调制器（MZM），并且一直是TFLN光子学面临的主要挑战之一22。

已经采用几种方法来减轻电光弛豫效应，从而克服电光MZM的偏置点漂移。这些方法包括在较低光功率下操作（<10 dBm）和使用具有热光效应的加热器来在所需偏置点下操作4,22，这两种方法限制了可用性和实用性，或者在某些应用中可能不可行。最近，我们小组6和其他小组10,12展示了通信波长TFLT MZM在性能上优于TFLN调制器。我们推断，对于芯片上光功率高达12.1 dBm时，TFLT的电光弛豫较慢6。

目前尚未展示TFLT在其他波长下的电光设备性能。特别感兴趣的是可见光和近红外波长23，这些波长与成像24、钟表25、数据中心26、显示27、光谱学28和量子信息29等应用相关。例如，受到这些动机的启发，TFLN MZM已在738 nm30、400-700 nm31、768 nm的上转换32和最近的456 nm33波长下开发。预计在接近LN带隙的较短波长下会出现更强的光诱导电光弛豫效应。

在这里，我们设计并制造了一种在737 nm近红外波长下工作的TFLT MZM，其在环境条件下表现出优于使用相似工艺制造的等效TFLN MZM的直流偏置稳定性。具体而言，我们在使用TFLT时，在16分钟内测得小于2 dB的激光功率波动，而在使用TFLN时则在相同时间尺度上测得为8 dB，泵浦功率为4.3 dBm，在四分之一偏置下直流偏置调制器。此外，我们的TFLT MZM具有低的半波电压-长度积（0.65 V·cm）、高的消光比（30 dB）、低的光学损耗（5.3 dB）和受探测器限制的带宽（20 GHz）。需要注意的是，737 nm波长的兴趣来源于钻石中的硅空位颜色中心（SiV−），这是领先的固态量子存储器之一34。为了进一步评估我们的TFLT波导的光学损耗，我们制造了环形谐振器，并测量了高达2.8×10⁵的光学品质因子，相当于0.5 dB/cm的传播系数。此测量在638 nm波长下进行，因为我们的737 nm波长激光的调谐范围有限。

II. 设备制造

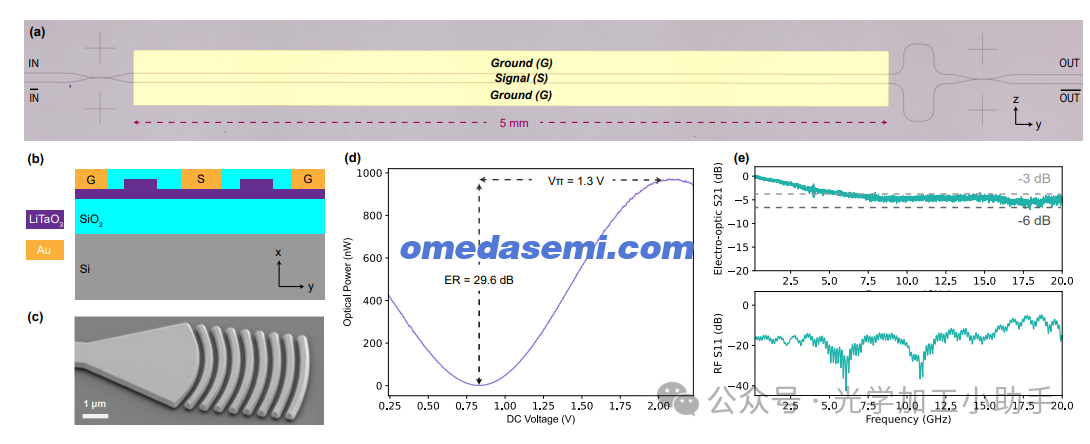
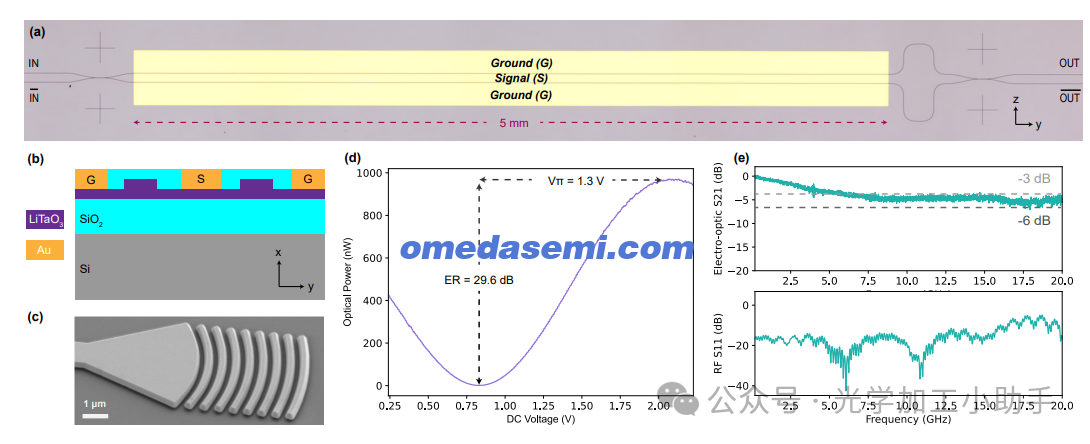
图1. 近红外薄膜钽酸锂马赫-曾德电光调制器
(a) 制造的调制器的光学显微镜图像。标出了晶体轴和电极细节。
(b) 调制器材料堆叠的横截面，晶体轴标示清楚。
(c) 扫描电子显微镜（SEM）图像，展示了用于将光耦合进出我们的调制器的光栅耦合器。
(d) 测量的调制器传输函数，应用电压缓慢变化，得到了29.6 dB的消光比（ER）和1.3 V的半波电压（Vπ）。
(e) 测量的电光频率响应（S21），受所用探测器的限制。调制器传输线的反射射频功率（S11）表明功率有效传输到电极。

图1a展示了制造的非平衡MZM的光学显微镜图像。它由一个方向耦合器作为输入光束分离器和一个长度为5 mm的电极（采用地-信号-地配置）组成，后面是另一个方向耦合器用于输出。光栅耦合器（图1a中未显示）用于将光耦合进出芯片，并连接到近红外单模光纤。选择方向耦合器的目的是最小化光学插入损耗，并且经过精心优化以实现50:50分光。

图1b展示了TFLT设备堆叠的横截面。设备的光学层是通过150 keV电子束光刻定义的，使用的是500 nm厚的ma-N2405光刻胶，涂覆在200 nm厚的x切TFLT-on-SiO2层上。波导宽度设计为600 nm。SiO2层的厚度为2 µm，并位于Si基板上。TFLT通过基于Ar+的感应耦合等离子体反应离子刻蚀（ICP RIE）刻蚀100 nm。使用高pH溶液去除刻蚀引起的再沉积物。随后，设备在520°C的O2气氛中退火2小时，以减轻刻蚀引起的缺陷。对于MZM，使用等离子体增强化学气相沉积（PECVD）沉积了800 nm厚的SiO2包覆层。用于评估光学损耗的环形谐振器保持未包覆状态。电极的沟槽通过375 nm光刻与SPR700-1.0光刻胶定义，并随后使用C3F8和Ar+气体进行干法刻蚀。通过电子束金属蒸发和剥离工艺定义电极（15 nm的钛层上覆盖800 nm厚的金）。所有MZM设备均在300°C下通过热板加热5小时，以去除可能对直流漂移效应产生负面影响的捕获电荷。TFLN MZM的制造采用类似工艺，具有相同的波导和电极几何形状。更多的制造细节请参见我们之前的工作6。

III. 结果
图1c展示了一个光栅耦合器的扫描电子显微镜（SEM）图像。使用超连续谱源和另一个带有光栅耦合器通过波导连接的芯片，我们估算该耦合器的3 dB带宽为35 nm，且每个耦合器的峰值效率为几个百分点（损耗为15.7 dB）。预计通过进一步的设计和制造改进，光栅耦合效率可以提高到30%（5 dB损耗）。接下来，使用737 nm的连续波激光光源，我们将光引导通过MZM，并估算其损耗为5.3 dB（不包括光栅耦合损耗），该损耗遍及28 mm的设备长度，包括光路波导。传输主要受金属吸收、弯曲损耗和制造引起的侧壁粗糙度的限制。

接下来，我们使用737 nm激光光源（芯片上功率为4.3 dBm）表征MZM的电光性能。首先，应用变化的赫兹频率电压，测得一个高的消光比29.6 dB（图1d）。这一比率表明，方向耦合器的分光比为49.5:50.5，接近最佳的50:50。此测量结果得出Vπ为1.3 V（图1d），对应一个低的0.65 V·cm VπL，这与TFLN近红外MZM30相当。然后，我们使用向量网络分析仪（VNA，Agilent E8364B）向调制器发送高频电信号。调制器在四分之一偏置下偏置，调制后的光信号被引导至一个20 GHz带宽的光电探测器。该探测器连接到VNA，形成电光（EO）测量回路。MZM的EO性能（S21）和电气反射（S11）如图1e所示。3 dB的EO滚降频率为约5 GHz，而在半波电压Vπ（即S21图中的6 dB线）方面的3 dB滚降频率超过了我们光电探测器的带宽。快速的滚降与平坦的高频响应相结合，表明我们的设备存在不完美的阻抗匹配，而非速度匹配问题。可以通过使用更厚的底部氧化层并重新设计电极（例如分段电极）来解决这一问题。阻抗不匹配也与S11中测得的强反射一致（图1e）。

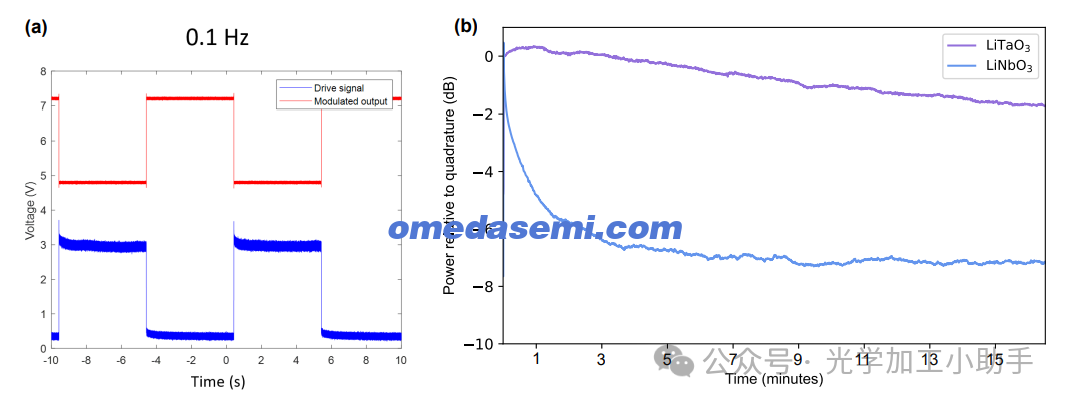
图2. 使用 (a) 施加的0.1 Hz方波信号和 (b) 电压阶跃测量薄膜钽酸锂马赫-曾德调制器的电光弛豫。在相同条件下，等效的薄膜锂铌酸调制器的弛豫速度更快。

接下来，我们测量了MZM在长时间尺度上的直流偏置稳定性。首先，我们使用737 nm的芯片上光功率为4.3 dBm，向调制器施加频率为0.1 Hz的方波，并通过光电探测器测量调制器响应。输入驱动信号和对应的输出光信号分别显示在图2a的红色和蓝色中。在这个频率下，电光弛豫效应难以观察到。因此，为了揭示较长时间尺度下的电光弛豫，我们向设备施加一个阶跃电压（从同相到四分之一偏置），并保持电压不变。使用4.3 dBm的芯片上光功率，我们测量了16分钟时间尺度内2 dB的光功率漂移（图2b）。我们使用等效的TFLN MZM进行相同的测量，在相同时间尺度上显示出8 dB的直流偏置漂移。

最后，为了进一步研究波导的光学传播损耗，我们制造了光栅耦合的239 µm直径微环谐振器。环形的波导宽度为1 µm。图3b插图展示了其中一个谐振器设备的SEM图像。由于我们737 nm激光的调谐范围有限，我们改为使用可调的638 nm波长激光并测量环形谐振器的共振光谱（图3a）。由于激光和耦合设置的多模输出，观察到激光功率波动（图3a插图），我们进行了校准，以清楚地观察到我们环形谐振器的205 pm自由光谱范围（图3a）。对共振线宽的拟合产生了2.7 pm的FWHM（图3b），对应的加载质量因子（Q）为2.8×10⁵。由于谐振器强烈过耦合，这近似为内在质量因子，且对应的损耗系数为0.5 dB/cm。我们调整了激光功率，确保共振线宽测量不受热光效应或光折射效应的影响。这个损耗系数与在TFLN中测量的结果相当30。

IV. 结论
我们展示了一种薄膜钽酸锂马赫-曾德电光调制器，具有缓慢的电光弛豫和0.65 V·cm的低半波电压长度积，适用于近红外光电子学应用。该调制器具有低光学损耗（5.3 dB）、30 dB的消光比和20 GHz的探测器限制带宽，后者适用于多个光谱学和原子应用，包括与钻石中的SiV−中心的接口。我们已在通信波长下演示的平衡MZM设计6，除了通过改进的材料加工策略（退火、掺杂、表面处理或不同的电极金属）进一步提高直流稳定性。