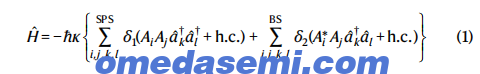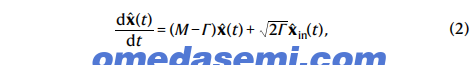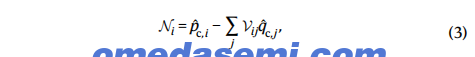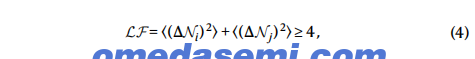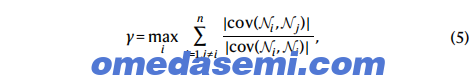专业高效
微纳加工公司

量子信息的基本单元是量子比特（qubit）或量子模式（qumode）。它们可以在离散变量或连续变量量子系统中进行物理表示，例如光学、原子、超导和机械系统。一个关键目标是纠缠大量的量子比特或量子模式。实现大规模光的纠缠对推进量子计算、网络和计量学等量子技术至关重要。普适的光学量子计算可以通过对大规模纠缠簇态进行一系列测量来实现。使用光时，量子比特通常编码在单光子的离散模式中，而量子模式则编码在光场的连续四分量中。单光子中的离散变量编码允许超高保真度的量子比特操作，但目前面临着确定性生成和纠缠量子比特的挑战。这导致了在离散变量实验中，使用概率性多量子比特纠缠的量子信息处理的令人印象深刻的演示。相比之下，光的四分量中的连续变量编码则允许确定性地生成和纠缠量子模式，但代价是较低的保真度。通过在不同自由度中多路复用光，例如路径、时间、频率和空间特征模，提供了一种创建大规模连续变量簇态的有前景的方法。

一片6寸=25个20*20小片，一片4寸=9个20*20小片

ALOOI晶圆；--氧化铝薄膜晶圆，键合工艺和镀膜工艺

TAOOI晶圆--氧化钽薄膜晶圆，镀膜工艺

SINOI晶圆；--超低损耗氮化硅薄膜晶圆，

SICOI晶圆；新型量子光学平台

6寸LTOI晶圆批量供应；铌酸锂的有力的竞争对手，薄膜钽酸锂晶圆

8寸LNOI晶圆;8寸LNOI助力更大规模薄膜铌酸锂产品量产

LN/LT-SOI/Si/SIN  W2W&D2W异质集成

流片： 6寸 氮化硅 铌酸锂 硅光 超高性价比流片， 1个BLOCK的价格买一整片晶圆

划重点--全国产-超高性价比-6 寸硅光-氮化硅-铌酸锂流片白皮书

集成量子光子学是一个多功能的平台，可以在芯片上编码、处理和存储光的量子信息。离散变量集成量子光子学（DVIQP）技术已产生用于单光子的集成源、电路和探测器、多量子比特真正纠缠，以及量子计算和网络中的原理验证演示。预计连续变量集成量子光子学（CVIQP）将提供高复杂性、相位稳定性、精确的模匹配、无需模清洁和低接口损耗，贯穿于光的四分量的生成、操控和检测。集成光子学材料和技术的最新进展显著推动了CVIQP的发展。它包括在光波导电路和微谐振器中观察到单模和双模四分量压缩态（即爱因斯坦-波多尔斯基-罗森（EPR）态）。在用于高斯玻色子采样的压缩器阵列中和在单一微谐振器基础上的频率梳中，已经演示了多个双模EPR态，其中只产生了双模纠缠。最近，已经在孤子微梳中研究了二阶单光子相关性，这意味着由自发参量过程主导的多模纠缠。然而，连续变量多量子模式或多方纠缠的生成和检测在集成量子光子平台中仍然未知。

在这里，我们报告了首次在集成光学量子芯片上生成的连续变量多方纠缠。我们操作了一种基于集成光学微谐振器的频率梳（即微梳），在低于阈值的量子频率模式下生成了多模高斯态。通过违反正部分转置（PPT）准则，我们展示了八个频率量子模式的不可分离性。我们表明，由于微梳中的布拉格散射效应，多方纠缠具有簇型结构不能直接在频率模式中生成，而是生成在超模中，这使得微梳中的多方纠缠机制与二阶压缩过程中的机制有所不同。我们采用了相干多色泵浦-探测（CPPD）技术，进行多方纠缠的准备、操控和测量，并保持系统中的相位相干性。通过实验违反van Loock–Furusawa准则，我们验证了多种超模多方纠缠的生成。通过测量具有总的非对角相关性约为对角相关性的4-8%的零点相关性矩阵，我们表征了生成态的纠缠结构，这些结构接近于有限压缩的对应簇型结构。此外，跨越广泛侧带频率检测到了四分量压缩和多方纠缠。我们的结果表明，在CVIQP芯片上生成和处理大规模纠缠的可能性，为可扩展的光子量子技术提供了前景。

图1 | 集成光学低阈值微梳中的连续变量多方纠缠。a，采用相干的多色相位锁定光学频率梳（实线）外部激发集成光学微谐振器。b，在微谐振器中，发生克尔非线性光学过程，这些过程在参量振荡阈值以下进行，量子频率模式（Qi，虚线）在微梳中出现。泵浦梳和微梳的自由光谱范围（FSR）满足 Δfpump = mΔfcavity（其中 m 是整数）。微谐振器可以通过上部微加热器进行控制，以匹配泵浦梳。参量过程，包括自发配对压缩和布拉格散射，在微谐振器中产生量子频率模式的复杂高斯态，这些态可以线性转换为特征超模（即 Qe1，Qe2，... Qen，一组频率模式的叠加），具有显著的内在压缩，进一步生成基于超模的多方纠缠态，具有各种簇型结构。c，可以生成多个超模的近似簇型态（即 Qc1，Qc2，... Qcn）。通过调整多色泵浦光束的配置和本地振荡光束的测量基，可以重新配置多方纠缠的结构。在多方纠缠态的图形表示中，蓝色顶点表示超模，黑色边表示等于1的确定性纠缠。

其中 x = (q1, q2, ..., qn | p1, p2, ..., pn)T 是四分量的向量，qk = a†k + ak, pk = i (a†k - ak)，xin 是输入场的四分量向量，满足输入输出关系 xin(t) + xout(t) = 2Γ(t)，M = [i Hint,] x /ħ，Γ = diag(γ1, γ2, …, γn | γ1, γ2, …, γn) 分别是增益和衰减矩阵。

在图1中，通过大量相位锁定的同步多色光束（例如来自外部相干光频率梳的光束）馈送激发，可以在微梳中生成大规模纠缠的多模高斯态。我们并不直接在频率梳模式（Q）中检测纠缠结构，而是提取特征超模（Qe），并使用它们在相应的超模（Qc）中生成具有各种结构的多模簇型态。超模可以视为频率梳模式的叠加，经过线性变换。通过基于特征超模测量态，可以表征内在的四分量压缩和多模纠缠的程度，这通过多色同相检测进行，调节本地振荡光束。此外，通过重新配置线性光学高斯变换（通过多色本地振荡器）和专用控制多色泵浦，可以重塑纠缠结构。CPPD方法能够精确高效地生成、操控和测量频率域中的大规模纠缠。在本研究中，我们以八个频率量子模式为例，基准化该过程。生成、操控和测量具有各种结构的超模多方纠缠态的过程已在补充信息第2.1节中提供。

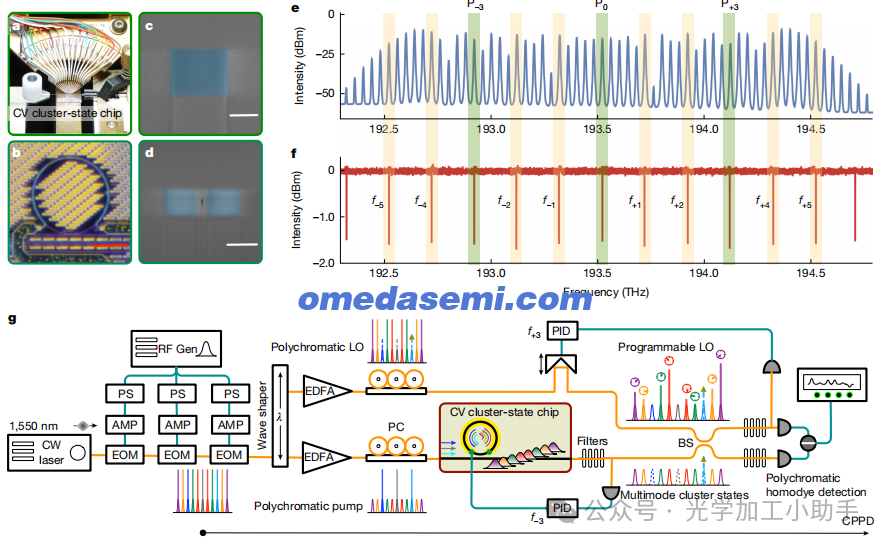
图2 | 集成硅氮化物微梳及其用于生成和表征连续变量多量子模式纠缠的实验装置。a，芯片载体的照片。芯片通过带透镜的单模光纤进行进出耦合。集成微加热器通过直流探针进行控制。b，制造的硅氮化物微环微谐振器的光学显微镜图像，半径为114 μm。c,d，扫描电子显微镜图像（伪彩色），显示单模波导的横截面为1 μm × 800 nm，且总线波导与微环之间的间隙为400 nm。e,f，电光梳和微环的测量光谱，分别具有39.98 GHz和199.9 GHz的自由光谱范围（FSR）。在电光梳中，P±3,0频率的光被选为泵浦（绿色窗口），而f±1,±2,±4,±5（橙色窗口）频率的光被选为本地振荡光束。在微谐振器中，在f±1,±2,±4,±5的频率下生成低阈值的多模高斯态。g，CPPD实验设置。一个低噪声连续波（CW）激光器（波长为1,550 nm）通过三级级联的电光调制器（EOM）调制，产生电光梳。一个波形器用于调整泵浦和本地振荡光束。三个泵浦用于同步激发微梳，以生成多模高斯态。采用多色同相检测，其中本地振荡光束的强度和相位被重新编程，用于表征和重新配置超模的多方纠缠态。量子噪声通过频谱分析仪记录。多色泵浦和用于同相检测的多色本地振荡器从同一个电光梳中分出，因此它们在整个系统中具有高度的相干性。RF Gen，射频发生器；EOM，电光调制器；AMP，电子放大器；EPS，电子相位移器；PC，偏振控制器；EDFA，掺铒光纤放大器；PID，比例积分微分；BS，光纤分束器；CV，连续变量。橙色线表示单模光纤，蓝色线表示电缆。比例尺：100 μm（b）；500 nm（c）；1 μm（d）。

图2a-d展示了在氮化硅纳米光子波导中制造的量子微梳设备。它被认为是一个有趣的集成量子光子平台，具有低光学损耗、强第三阶非线性、高密度集成和互补的金属氧化物半导体兼容性。在微环谐振器中，通过调整波导的结构色散实现了异常色散（补充图1）。大约200 GHz的自由光谱范围（FSR）的模式间距使得梳状光谱之间良好的分离，抑制了参量荧光噪声和非参量效应。采用过耦合方法从腔体中高效提取（约90%）压缩光。补充图1中测得的高内在质量因子为100万。在实验中，微环通过上部热光电阻微加热器调节，以将谐振频率（图2f）锁定到电光（EO）泵浦梳（图2e）的频率，这些梳光谱是通过调制1,550.245 nm（193.518 THz）超低噪声激光产生的。电光梳的梳间距与微梳的模式间距对齐，具有Δfcavity = 5ΔfEO。

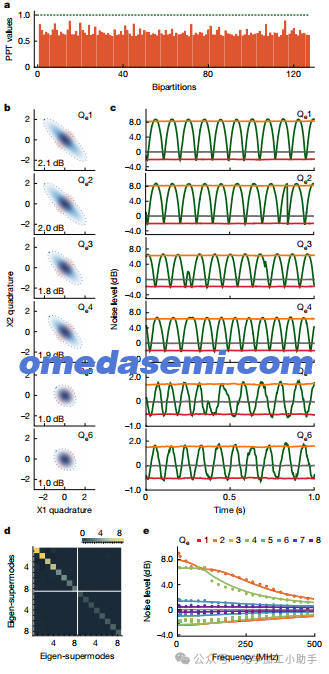
图3 | 多模压缩的生成与表征。
a，八模高斯态在频率梳模式中的所有二分割的实验辛特征值。所有辛特征值的估计值均低于1（绿色虚线），实验上违反了所有二分割的PPT准则。
b，六个主导特征超模（即Qe1–Qe6）的相位图。蓝色椭圆表示四分量压缩和反压缩，而红色圆点表示真空波动。
c，六个特征超模的噪声功率的直接实验测量。灰色线表示射击噪声水平，绿色线是通过定期调整本地振荡器相位测得的噪声曲线。红色线是通过压缩并锁定相位测得的，橙色线是通过反压缩并锁定相位测得的。
d，八个特征超模（即Qe1–Qe8）的测量协方差矩阵。矩阵通过颜色编码，顶部有键值。
e，八个特征超模在不同侧带频率下的四分量压缩和反压缩。点表示实验数据，线表示方程(2)的理论结果。理论上，超模是双重简并的，而在实验中它们是可以区分的（通过两个相似颜色的点表示）。a–d中的数据是在5 MHz侧带频率下收集的。

图2g展示了CPPD实验设置。多色泵浦和多色同相检测技术的使用在创造首次（据我们所知）专门在频率域内实现的集成光学连续变量多方纠缠中起到了至关重要的作用，而不是其他方法。我们的CPPD结合了这些先进技术，通过多色泵浦和检测过程实现了全局相位锁定。使用波形器，P±3,0的电光梳用作同步多色泵浦的相位锁定泵浦，而f±1,±2,±4,±5的梳光则作为多色同相检测的本地振荡器。由于电光梳的相干特性，压缩光束和本地振荡光束的相位固有地稳定。此外，f+3的梳光与后分束器干涉，被重新用作参考，用于全局锁定本地振荡器和压缩光束之间的相对相位。这种方法使得能够在统一的全局相位锁定参考框架内精确测量四分量压缩、多模纠缠，并全面表征生成态的协方差矩阵。在实验中，通过调整本地振荡器的强度和相位，实现了单色、双色和多色同相检测（补充图3）。我们选择5 MHz作为实验中的基本侧带频率，以准确表征四分量压缩和多方纠缠。更多细节请参见补充信息第1节。

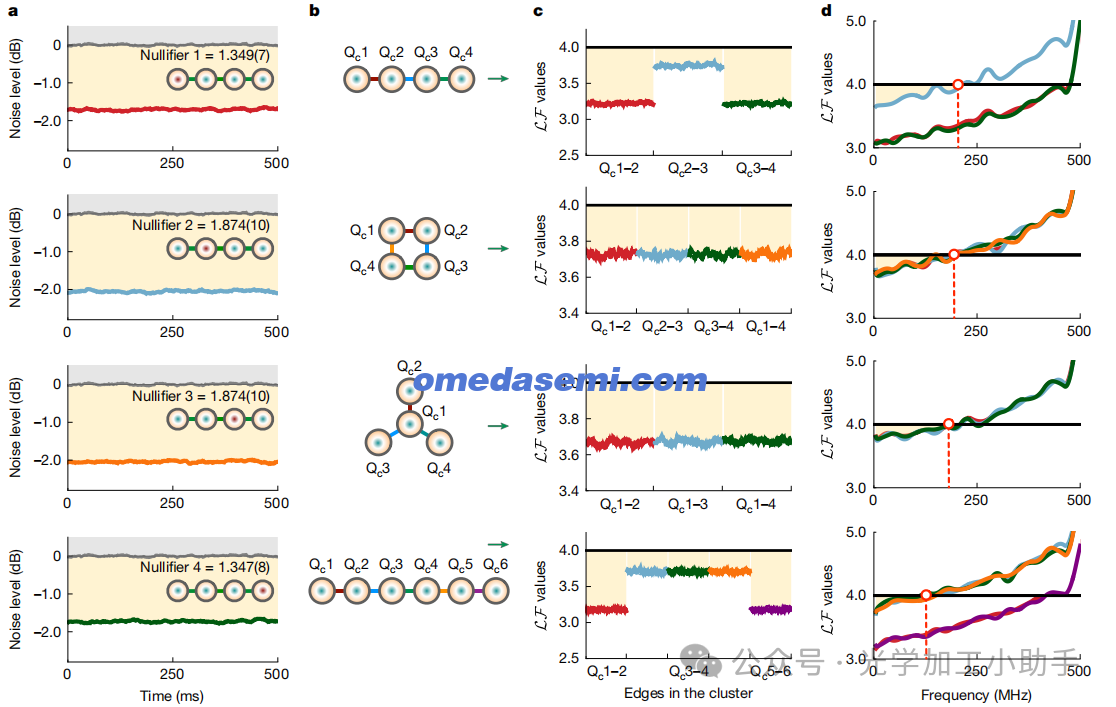
图4 | 零点算符的实验测量和van Loock–Furusawa不等式的违反。
a，线性类型纠缠结构的四个零点算符的噪声功率的直接实验测量。零点方差{1.349(7), 1.874(10), 1.874(10), 1.347(8)}已归一化到射击噪声（灰色线），分别重新缩放为{2, 3, 3, 2}。括号中的值表示±1σ不确定性，每个不确定性是从一组400个数据点估算的。射击噪声上的灰色区域表示没有压缩，而橙色区域表示存在强压缩。
b，超模（Qci）中各种簇型纠缠结构的图形表示，包括线性、盒型和星型纠缠结构。
c,d，在c中，5 MHz侧带频率下测量的LF值，以及在d中不同侧带频率下测量的相应纠缠态的LF值。如果测量的LF值小于4，则不等式被违反。c和d中的彩色数据表示在b中不同边缘的测量不等式。如果所有边缘的不等式都被违反，我们确认成功生成了多方纠缠。在c和d中，在橙色区域，所有van Loock–Furusawa不等式都被实验上违反，证明了在广泛频率下存在多方纠缠。

我们首先通过实验违反连续变量版本的PPT准则验证了八个频率模式的纠缠。如果复合系统的状态可以分解为两个子系统的积态，那么对一个子系统进行部分转置仍然会生成一个具有大于或等于1的辛特征值的物理状态。相反，如果部分转置后的状态具有小于1的辛特征值，则原始状态被证明是不可分离的。对于八个量子模式的高斯态，总共有127种不同的二分割，包括{1×7, 2×6, 3×5, 4×4}二分割。图3a展示了从频率模式中测量的协方差矩阵估算的部分转置状态的辛特征值（见补充图4）。对于所有127种二分割，辛特征值均小于1，这表明八个量子模式的状态不能分解为两个独立子系统的积态。因此，违反PPT准则证明了多方纠缠的存在。芯片上的内在八量子模式状态也预期具有更强的纠缠（补充图7）。

通过应用补充图4中测量协方差矩阵的Bloch–Messiah分解，我们提取了特征超模基。实验中，我们进行了多色同相检测，以直接表征所有八个特征超模的压缩。例如，图3b和图3c展示了为准备簇型结构的多方纠缠而选择的六个主导压缩的特征超模的测量结果。它获得了四个约2 dB的压缩超模（芯片上为6 dB），以及两个约1.0 dB的压缩超模（芯片上为2.6 dB）。每个超模的芯片内在压缩和多色检测中LO梳光的配置见补充图4。所有八个特征超模的测量协方差矩阵报告在图3d中，显示了超模的基本正交性，并且具有最小的非对角项，这对于生成和验证多方纠缠态至关重要。我们指出，在频率模式中，补充图4中的协方差矩阵显示了强烈的非对角相关性，源自微梳中的内在布拉格散射效应，这意味着通过任何高斯局部单位操作，在频率模式中直接生成具有簇型结构的多方纠缠是不可实现的（补充信息第2.4节）。相反，这种纠缠的生成可以在微梳的超模中发生，通过对选定的特征超模应用非局部多模操作（补充信息第2.1节和补充图5）。图3中的结果表明了多模压缩的一个实例，而特征超模压缩器的压缩强度将通过重新配置多色泵浦来为各种纠缠结构量身定制。

其中下标c表示变换后的Qc超模。在我们的实验中，我们对多色本地振荡器进行了线性操作（相当于对多模高斯态应用线性变换），并精细调整了多色泵浦的强度和失谐，以获得理论上获得的特征超模压缩器的压缩强度，从而准备具有簇型结构的多方纠缠。

然后，我们验证了对于具有不同纠缠结构的多方纠缠态违反van Loock–Furusawa不等式的情况。

其中LF代表在实验中测得的van Loock–Furusawa值。图4a报告了具有线性类型纠缠结构的四超模纠缠态的四个测量零点算符（归一化到真空波动）。获得的零点方差为{1.349(7), 1.874(10), 1.874(10), 1.347(8)}。括号中的值表示±1σ不确定性。由此导致实验上违反了所有三个van Loock–Furusawa不等式，值为{3.223(13), 3.748(17), 3.221(13)}，如图4c所示。这些不等式的违反成功地展示了线性类型的多方纠缠结构。此外，我们还实验性地测量了四超模盒型和星型纠缠结构的零点算符和不等式，以及六超模线性类型纠缠结构，如图4b所示。测量的LF值结果报告在图4c中。已验证最多六个超模的多方纠缠态，具有不同的纠缠结构，能够违反这些不等式。零点算符和不等式的完整集合及其实验结果见补充表2。

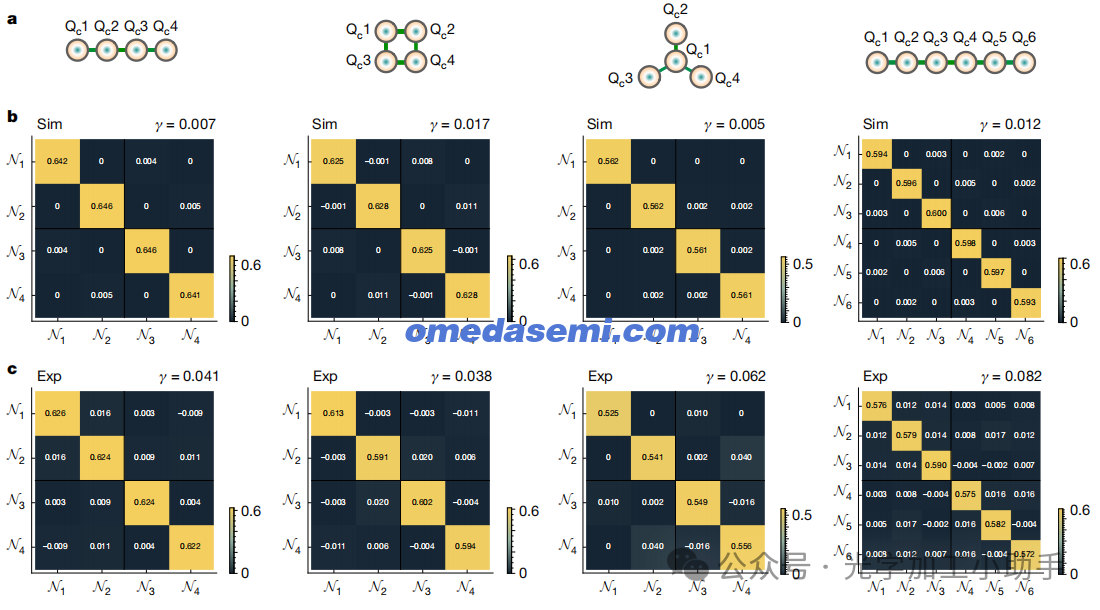
图5 | 各种多方纠缠的零点算符相关性的全面表征。
a，线性、盒型和星型纠缠结构的图形表示。变换后的超模表示为Qci。
b，模拟结果。
c，实验结果，显示芯片上生成的纠缠态的零点相关性完整矩阵，包含线性、盒型和星型纠缠结构。模拟结果是根据每个纠缠结构的特征超模的压缩分布估算的。所有矩阵与通过常数λ缩放的单位矩阵非常相似，如补充表1所示。顶部显示的相应γ值表明，与对角相关性相比，我们的模拟和实验中的非对角相关性明显较低。零点相关性矩阵通过其绝对值（|cov( , N Ni j)|）以颜色编码，并在右下角提供了颜色键。每个元素的值已明确显示以提高清晰度。

此外，由于不等式（方程(4)）的违反不足以表征生成态中的全部纠缠信息，特别是对于有限压缩的情况，我们通过测量推导出的芯片上态的零点相关性完整矩阵进行了综合分析。结果显示在图5中。图中表明，非对角相关性明显低于对角相关性。这是由于泵浦配置进行了精确调整，以匹配不同状态下压缩器的压缩强度。为了量化可能未被生成状态的簇型结构捕获的额外隐藏纠缠的程度，我们引入了一个γ因子，用于描述相对于对角相关性，非对角相关性的总和被抑制的程度。

其中 ∣cov(Ni, Nj)∣ 代表零点算符相关性的绝对值。在优化的压缩分布下，图5c中报告的四个生成态的相关矩阵和相应的γ值{0.058, 0.048, 0.101, 0.109}是我们实验中测得的，这与图5b中基于测量的特征超模压缩分布所推导的模拟结果一致。图5b中的模拟结果表明，对于当前实验泵浦配置，γ的最佳可实现值为{0.007, 0.019, 0.006, 0.016}。理论上从对角矩阵的偏差来源于多色泵浦和多色本地振荡器配置与其理想设置之间的轻微偏差。这些结果表明，簇型结构有效地捕捉了我们实验中几乎所有的纠缠信息，紧密地接近了相应簇型态的特征。未来对实验系统的改进将使生成的多方纠缠能够更加准确地表征。更多细节请参见补充信息第2.1节和3.3节。

观察到的四分量压缩和多方纠缠强烈依赖于其测量中涉及的侧带频率。侧带的过多噪声分布可能会破坏低侧带频率下的压缩和纠缠。此外，在布拉格散射效应的存在下，高侧带频率下的真实协方差矩阵可能远离实对称矩阵，而是厄米矩阵，并且不能完全通过同相检测捕获。图3e显示了在广泛侧带频率下测得的八个特征超模的压缩水平，从它们的测量协方差矩阵中估算得出。考虑到标准同相检测的不完全性，量子朗之万方程（2）建模的理论结果（包括系统损耗）与实验结果良好一致（图3e）。在广泛的侧带频率范围内，观察到大于1 dB的显著四分量压缩。此外，在图4d中，在不同的侧带频率下，我们测量了不同簇态的不等式违反情况。对于所有四超模簇态（线性、盒型和星型簇态），在约200 MHz侧带频率下都成功地违反了不等式，而对于六超模线性簇态，在约100 MHz侧带频率下也成功违反了不等式。这些结果表明，多量子模式纠缠对低频过多噪声具有较强的鲁棒性，这对实际应用至关重要。

总之，我们展示了在集成光学微梳中芯片尺度上确定性地生成连续变量多方纠缠，并通过实验违反van Loock–Furusawa准则验证了纠缠。我们测量了完整的零点相关性，以表征生成态的多方纠缠结构，这些结构与相应的簇型结构非常接近。通过深入探讨微梳中多方纠缠生成的物理机制，并结合先进的多色泵浦-检测方案和技术的相干集成，使得这一展示成为可能。尽管我们使用的是小规模的纠缠态和适度的压缩水平，但利用集成光子的独特能力，为进一步扩展和增强开辟了新的途径（见补充信息第4节的讨论）。通过使用更大的微梳尺寸、宽带微梳或将孤子梳用作多色泵浦，可以促进将纠缠量子模式的数量扩展到数百或数千。此外，在集成光子平台上通过路径和时间模式多路复用频率模式，为进一步增加纠缠态的规模提供了路径。通过优化超高Q微谐振器中压缩光束的逃逸效率，可以实现更强的压缩。CVIQP技术的可扩展性和能力最终可以通过将连续变量量子光源、线性光学量子电路和同相探测器，以及DVIQP设备如单光子源和光子数分辨探测器进行共集成来解锁。离散和连续变量混合集成量子光子学的发展为可部署的芯片尺度量子传感、实际量子网络和普适量子计算提供了机会。

Xinyu Jia1,2,9, Chonghao Zhai1,9, Xuezhi Zhu3,9, Chang You1, Yunyun Cao3, Xuguang Zhang4,

Yun Zheng1, Zhaorong Fu1, Jun Mao1, Tianxiang Dai1, Lin Chang4, Xiaolong Su3,5 ✉,

Qihuang Gong1,5,6,7,8 & Jianwei Wang1,5,6,7,8 ✉

单位：

1

State Key Laboratory for Mesoscopic Physics, School of Physics, Peking University, Beijing, China. 2Beijing Academy of Quantum Information Sciences, Beijing, China. 3State Key Laboratory of

Quantum Optics Technologies and Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan, China. 4State Key Laboratory of Advanced Optical Communications System and Networks,

School of Electronics, Peking University, Beijing, China. 5Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, China. 6Frontiers Science Center for Nano-optoelectronics &

Collaborative Innovation Center of Quantum Matter, Peking University, Beijing, China. 7Peking University Yangtze Delta Institute of Optoelectronics, Nantong, China. 8Hefei National Laboratory,

Hefei, China.