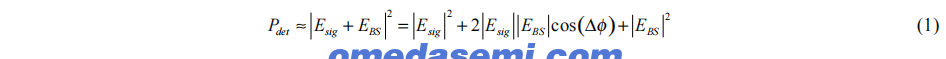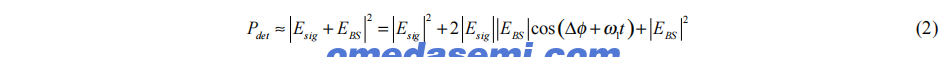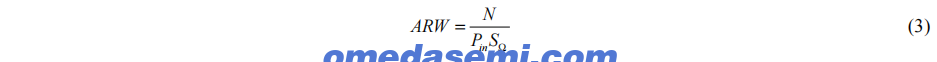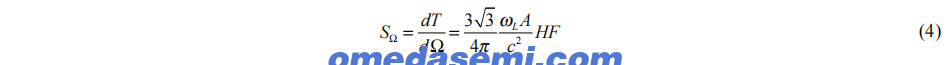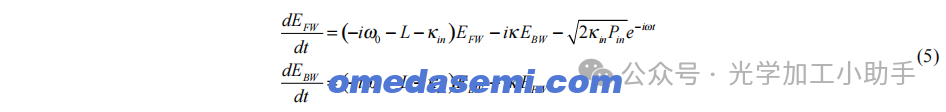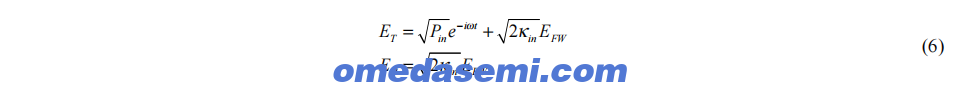专业高效
微纳加工公司

摘要  

硅光子技术的最新突破可能很快实现大规模生产的芯片级战术级（或更优）陀螺仪，通过使用与CMOS兼容的制造工艺来制造高度集成的高灵敏度光学陀螺仪。本文报告了我们在设计和构建光学陀螺仪方面的进展，该陀螺仪采用周长为37毫米、精细度为1270（本征品质因数为10^8）的SiN跑道形谐振器，并使用现成的光纤组件（环行器、分束器和调制器）和半导体激光器，实现了80度/小时/√Hz的角度随机游走（ARW），即1.3度/√小时。据我们所知，这是基于Sagnac效应的芯片级陀螺仪在单位面积上的ARW记录，比现有水平提高了2倍。我们采用了平衡检测方案，以消除由激光相位噪声通过谐振器中的残余背向散射转换为幅度噪声引起的18 dB陀螺仪噪声。研究发现，背向散射系数对波长非常敏感，因此对用于探测谐振器的谐振波长也非常敏感。测得的最低背向散射系数比平均值低1000倍以上。使用该谐振波长以及非对称相位调制方案，大大降低了陀螺仪的背向散射噪声。要实现该陀螺仪的理论最小ARW值16度/小时/√Hz，可能需要更低的背向散射系数或更好的背向散射噪声消除方法。进一步提升至战术级性能（或更优）可能需要更大的谐振器面积、进一步降低背向散射和/或使用频率噪声更低的激光器。

关键词：光学陀螺仪，硅光子学，光学谐振器，计量学，旋转传感，背向散射。

划重点--销售晶圆和加工

ALOOI晶圆；--氧化铝薄膜晶圆，键合工艺和镀膜工艺

TAOOI晶圆--氧化钽薄膜晶圆，镀膜工艺

SOI晶圆--硅光晶圆，键合工艺，可以定制

SINOI晶圆；--超低损耗氮化硅薄膜晶圆，库存和定制

SICOI晶圆；新型量子光学平台，纯定制

6寸LTOI晶圆批量供应；铌酸锂的有力的竞争对手，薄膜钽酸锂晶圆

8寸LNOI晶圆;8寸LNOI助力更大规模薄膜铌酸锂产品量产

LN/LT-SOI/Si/SIN  W2W&D2W异质集成

EBL和6寸 150nmDUV加工微纳结构

我们为客户提供晶圆（硅晶圆，玻璃晶圆，SOI晶圆，GaAs，蓝宝石，碳化硅（导电，非绝缘），Ga2O3,金刚石，GaN（外延片/衬底）），镀膜方式（PVD,cvd,Ald，PLD）和材料（Au Cu Ag Pt Al Cr Ti Ni Sio2 Tio2 Ti3O5，Ta2O5,ZrO2,TiN，ALN镀膜刻蚀,ZnO,HfO2。al2o3。更多材料），键合（石英石英键合，蓝宝石蓝宝石键合）光刻，高精度掩模版，外延，掺杂,电子束直写等产品及加工服务(请找小编领取我们晶圆标品库存列表，为您的科学实验加速。

请联系小编免费获取原文

1. 引言

随着自动驾驶汽车和其他小型自动化车辆的出现，迫切需要一种新的小型化、低成本、大规模生产的高灵敏度陀螺仪，以满足这一巨大需求，提供不依赖全球定位系统的紧凑型导航系统。此类应用需要一款噪声为大约0.1度/小时/√Hz的角随机游走（ARW）和漂移约为0.1度/小时的陀螺仪。MEMS陀螺仪在尺寸、成本和大规模生产方面符合要求，但由于其对冲击、温度和振动的敏感性，它们在这些环境下难以维持漂移要求。另一方面，基于Sagnac效应的光学陀螺仪对冲击和振动的敏感性较低，因为它们依赖于光的干涉，而不是惯性质量的运动，这使得它们成为一个很好的候选者。大多数商业化的光学陀螺仪要么是干涉型光纤陀螺仪（FOG），要么是氦氖激光环形陀螺仪（RLG）。根据不同的等级，FOG可能使用几十米到几公里的偏振保持光纤作为其Sagnac环路，使其体积较大，通常在1升左右。氦氖RLG则使用气体管和高电压电极提供激光增益，体积与FOG相似。尽管这两种光学陀螺仪的性能都非常优异，但它们目前并不符合低成本和小型化的要求。硅光子学技术的最新进展提供了将整个光学陀螺仪集成到单一芯片上的可能性，从而使得微型光学陀螺仪能够廉价大规模生产。我们工作的一个主要问题是，是否可以通过基于CMOS兼容技术的芯片级陀螺仪实现足够的噪声、漂移和稳定性，以满足自驾车、无人机甚至最终飞行器导航等应用的要求。

利用Sagnac效应的光学陀螺仪主要有三种类型。在所有这些类型中，光通过一圈光纤或光波导传播，当光纤或波导围绕其主对称轴旋转时，光会经历一个Sagnac相位偏移。干涉型光学陀螺仪通过两波Sagnac干涉仪测量这个Sagnac相位，而环形激光陀螺仪和共振光学陀螺仪则使用光学共振器，并通过测量共振频率的变化来反映这一相位偏移。由于Sagnac相位偏移非常微弱，并且与环路所围成的面积成正比，因此FOG必须使用多个光纤环路来增加Sagnac相位，从而提高响应。共振光学陀螺仪则使用一个环形共振器，光在同一个环路内多次传播，这样通过F/2（其中F为共振器的精度）来增强Sagnac相位。因此，它们通常不需要多个环路。RLG也通过使光在激光腔内多次循环来增强Sagnac相位。然而，在非常小的旋转速率下，它们会受到锁相效应的影响，这时背向散射导致陀螺仪对微小旋转失去敏感性。为克服锁相效应，RLG通常采用机械抖动，通过每秒几度的旋转来避免此问题。然而，这种解决方案会增加复杂性并降低可靠性和使用寿命。

文献中已经报道了三种类型光学陀螺仪的微型化版本。在[2]中，使用一个直径为7毫米、Q因子为109（精度为105）的CaF2共振器，演示了一个噪声为1.2度/小时/√Hz、漂移为3度/小时的共振光学陀螺仪。尽管该共振器非常小，但该陀螺仪不完全适合集成，因为需要一个棱镜耦合器将超窄线宽的激光自由空间耦合到共振器中。在[3]中，基于高Q（> 108）的二氧化硅楔形共振器，采用双向泵浦激发反向传播的激光信号，通过受激布里渊散射进行激发，构建了一个芯片级的RLG，取得了噪声为4.1度/小时/√Hz、漂移为3.6度/小时的结果。这一令人兴奋的结果是第一次用芯片级陀螺仪测量地球的自转。然而，二氧化硅楔形共振器在二氧化硅-空气界面传播光，这使得它对灰尘和表面划痕非常敏感，从而降低了陀螺仪的鲁棒性。此外，由于布里渊频移的温度依赖性，陀螺仪还经历了显著的热漂移[3]。在[4]中，报道了一种长为7.9厘米、Q因子为1500万（精度为197）的硅上二氧化硅环形共振器光学陀螺仪，具有720度/小时/√Hz的ARW和15度/小时的漂移。在[5]中，该小组进一步报道了一种具有4.08厘米直径、Q因子为1400万（精度为38）的硅上二氧化硅多圈共振光学陀螺仪，具有20度/小时/√Hz的ARW。另一项研究报告了一种利用50圈SiN波导（损耗小于0.78 dB/m）的干涉型陀螺仪，外径为4厘米，具有511度/小时/√Hz的噪声和58.7度/小时的漂移[6]。

由于在共振器中Sagnac相位被F/2增强，因此在本研究中我们选择使用一个具有超高精度的短、超低损耗的SiN波导，并利用高Q因子来最大化这种共振增强。该共振器采用CMOS兼容的工艺制造，如图1a所示。芯片上有多个器件，但只有顶部的赛道共振器被使用。其尺寸为2毫米×18毫米，周长为37毫米，相当于一个半径为5.8毫米的圆形环。该单模SiN波导（见图1b中的横截面）厚度约为100纳米，宽度约为2.8微米。波导上生长了一层氧化层，以保护它们免受灰尘和表面划痕的影响，从而放宽了封装要求。该赛道在约1.5微米波长下的传播损耗为0.4 dB/m，内在Q因子为108，精度为1270。与之前的共振器陀螺仪报告相比，这一精度显著更高，因为该共振器更小，这减少了往返损耗。具体来说，封闭的区域比[3]中的小40倍，比[4]中的小5倍，这导致我们陀螺仪中由给定旋转速率引起的Sagnac相位偏移变得更小，比例相同。

本文展示了通过在一种具有极低背向散射的特殊共振波长下工作，可以将背向散射系数抑制1,000倍，从而将陀螺仪的噪声降低至80度/小时/√Hz。噪声预计为8.3度/小时/√Hz，并受限于用于探测共振器的10 kHz线宽激光器的激光频率噪声。然而，背向散射噪声似乎仍然是限制噪声的主要因素。尽管如此，当噪声归一化到赛道的足迹面积时，其噪声仍然是[3]的两倍小，而且这种平台更适合低成本的大规模生产。与已报道的具有相似鲁棒性和适合大规模生产的芯片级陀螺仪相比，按面积归一化后，本文报告的噪声比[5]小约3倍，比[4]小约40倍，比[6]小约80倍。

2. 硅氮化物陀螺仪性能
2.1 实验陀螺仪配置

如图2所示，陀螺仪的示意图。可调半导体激光器（Pure Photonics PPCL301）发出的约1.5微米的光，通过电光调制器（EOM 1）进行频率调制，然后通过一个50/50光纤耦合器进行分光。耦合器的两个输出分别通过环形器，再分别进入芯片上的单模SiN赛道共振器，沿顺时针（CW）和逆时针（CCW）方向传播。这一耦合通过V型槽光纤连接器实现，每个光纤面损耗约6 dB。50/50耦合器的上臂还通过第二个电光调制器（EOM 2）来抑制背向散射噪声和漂移，如后文所述。

每个输入端的环形器将从赛道出来的光引导到陀螺仪输出端（标记为CW输出和CCW输出）。一个90/10光纤耦合器将CW输出的10%送到探测器（PD），其电输出进入伺服回路，锁定激光器到CW赛道共振，如下段所述。CW输出的其他90%送到差分（或平衡）探测器（New Focus 2117）。图2中来自底部环形器的CCW输出被送到差分探测器的另一端口。差分探测器测量CW和CCW电信号之间的差异，进而计算旋转速率。除了光子学芯片，所有其他组件均为现成的组件，带有偏振保持光纤和APC连接器。

Pound-Drever-Hall (PDH) 激光锁定技术被用来将激光锁定在赛道的CW共振频率上。这个过程通过用电光调制器（EOM 1）调制激光的频率，通常在约1 MHz的频率下进行，并通过锁相放大器（LIA）对CW探测器的电输出进行解调，以恢复该频率下输出分量的幅度。LIA的输出提供了一个误差信号，这是一个与激光频率偏移共振器CW共振频率成比例的直流电压。然后，这个误差信号被输入到一个比例-积分-微分（PID）控制器中，PID控制器根据这个误差信号应用所需的电压，控制激光的PZT控制器，从而调整激光频率以匹配共振频率。当旋转Ω作用于赛道共振器时，CW共振频率从静止时的频率ω0偏移到ω0 + ωs，其中ωs是由Sagnac效应引起的赛道共振频率的偏移。PDH伺服回路随后将激光频率修正为这个Sagnac偏移后的共振频率。然而，CCW共振频率在相反的方向上发生偏移，从ω0到ω0 − ωs，因此激光频率与CCW共振频率偏离了2ωs。因此，通过解调CCW输出信号，可以生成与2ωs成比例的信号，用于测量旋转速率。

在没有Sagnac相位偏移（即没有施加旋转）或其他非互易信号的情况下，当环温变化时，CW和CCW共振频率会以相同的量和相同的符号发生偏移，PDH伺服回路会纠正激光频率，使其保持锁定在CW共振频率上。此时，CW输出会显示出EOM 1调制频率的信号。但由于CCW共振也被锁定，CCW输出也会在调制频率下显示相同的信号。通过从CCW输出中减去CW输出，平衡探测器能够抑制（理想情况下是完全抑制）这一热源引起的漂移，因为它至少部分减少了其他常见的噪声和漂移源。

为了最大化这种共模噪声抑制，必须尽可能精确地平衡CW和CCW输出中的功率。激光到每个平衡探测器输入的光程也必须很好地匹配。如2.4节所示，通过平衡探测实现了18 dB的噪声抑制。然后，差分探测器的输出通过LIA解调，提取EOM 1调制频率下的分量，并将该信号发送到数据采集单元（DAQ）。

图2中陀螺仪设置中的第二个电光调制器（EOM 2）用于抑制背向散射噪声和漂移。背向散射会通过将CW波的一个小部分耦合到CCW方向，反之亦然，从而在陀螺仪的输出中引入噪声。因此，图2中每个输出（CW和CCW）是信号场Esig和背向散射场EBS的相干总和。因此，在每个输出端检测到的功率为：

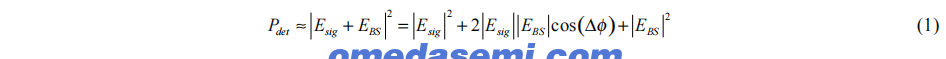
图1. (a) 用于陀螺仪的SiN赛道共振器的照片。(b) SiN波导的横截面。

其中Δφ是信号场Esig和背向散射场EBS之间的相位差，这个相位差由于热路径长度的变化可能随时间漂移，从而引起噪声和漂移。由于主信号和背向散射信号中的光子是在激光器中不同时间产生的，激光相位噪声会映射到Δφ中的噪声，从而通过方程（1）中的余弦项在陀螺仪输出中产生幅度噪声。|EBS|²项也包含噪声和漂移，但在背向散射较小的陀螺仪中，这些通常可以忽略不计，因为|EBS|远小于|Esig|，且方程（1）中的余弦项远大于|EBS|²。

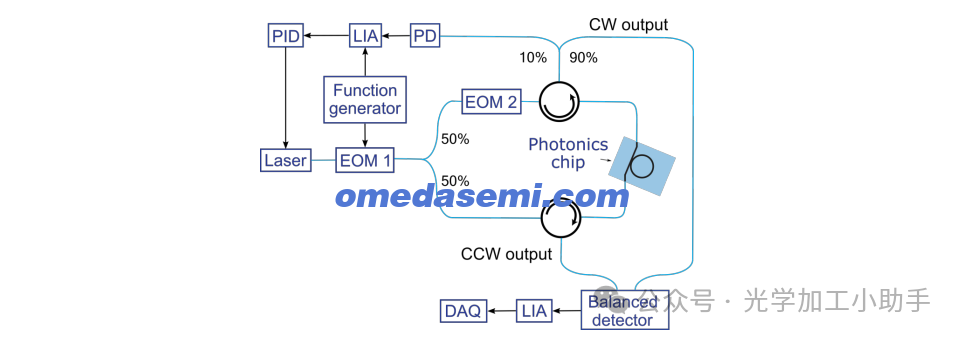
图2. 陀螺仪架构示意图。蓝色线条表示单模保偏光纤，黑色箭头表示电连接。光通过V槽连接的光纤耦合到芯片环形共振器波导的两个端口。激光器是Pure Photonics（PPCL301）生产的InP外腔激光器，工作波长约为1550纳米。PD = 光电探测器，LIA = 锁相放大器，EOM = 电光相位调制器，PID = 比例-积分-微分控制器。

为了抑制背向散射噪声和漂移，EOM 2通过微小的频率ω1调制CCW光的光学频率（相对于共振线宽来说很小），使信号场和背向散射场在光学频率上有所不同。这使得在每个输出端检测到的功率随之变化为：

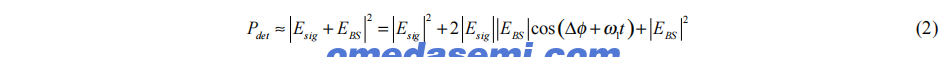
频率ω1被选择为足够大，以使方程（2）中的余弦项足够快速地振荡，以便被陀螺仪的读出电子设备滤除，从而抑制背向散射噪声和漂移。另一种解释这种效应的方式是，相位调制频率ω1的光会在ω1的整数倍处产生边带；入射到EOM上的载波频率ω0的光被移到频率ω0 ± mω1处，其中m是整数。为了最大化噪声抑制，至关重要的是最小化保留在ω0的光，因为它是载波频率与沿相反方向传播的主信号之间的干涉，导致背向散射噪声。这个载波最小化是通过适当选择相位调制幅度来完成的。保留在载波频率上的光与J0(πV/Vπ)成正比，其中J0是第一类零阶贝塞尔函数，V是施加到EOM的电压幅度。所有光因此会移到边带（并且没有光保留在载波中），当πV/Vπ等于J0的零点时，其中Vπ是EOM的半波电压。满足这一条件的最小电压为V ≈ 0.765Vπ。因此，图2中的EOM 2以30 kHz的正弦波进行调制，电压幅度为其Vπ的76.5%。

2.2 陀螺仪角随机游走（ARW）的理论预测
本节提供了对陀螺仪角随机游走（ARW）的理论预测。噪声的主要来源是背向散射噪声、激光频率噪声、探测器噪声、激光的相对强度噪声（RIN）和光子噪声，这些都可以根据陀螺仪中使用的元件的规格进行计算（见图2）。我们不知道已发布的有关共振陀螺仪中由于共振器背向散射引起的噪声的模型，因此在这个预测中没有考虑背向散射噪声。正如将在第2.4节中展示的，背向散射噪声似乎是该陀螺仪中占主导地位的噪声源，因此这些ARW预测作为理论极限，当背向散射噪声被抑制到低于上述噪声源时。
ARW的定义是噪声与信号的比率，计算公式为：

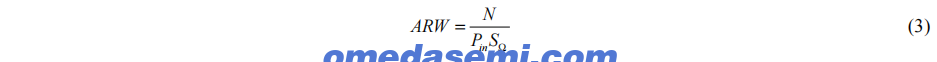
其中N是检测到的电信号中的总噪声功率，Pin是输入到环形谐振器中的激光功率，SΩ是旋转灵敏度。

对于图2中的陀螺仪，旋转灵敏度取决于EOM 1施加的光频率调制深度。这种频率调制使得激光频率在共振峰的尖端沿着正弦波回摆，保持在共振的中心位置，这要归功于PDH锁定。当激光频率被深度调制时，旋转灵敏度较大，因为此时激光频率在共振的边缘花费较多时间，而该处的传输斜率较陡。然而，由于该陀螺仪在共振时传输最小，对于较浅的频率调制，平均检测功率较小，因为激光频率更多时间停留在共振尖端附近。以这种方式减少平均检测功率可以降低相对强度噪声（RIN），因为它与平均检测功率成正比，并且降低光子噪声，因为光子噪声与检测功率的平方根成正比。然而，这种噪声减少是以降低灵敏度为代价的。因此，频率调制深度可以进行优化，以最小化方程（3）中的ARW。本文报告的陀螺仪噪声和漂移在最大旋转灵敏度下最低，因此EOM 1被调节，直到PDH误差信号最大化，正如在[4]中所示。通过[10]中的旋转灵敏度表达式可以很容易地证明，在EOM 1的最佳频率偏置下，旋转灵敏度给定为：

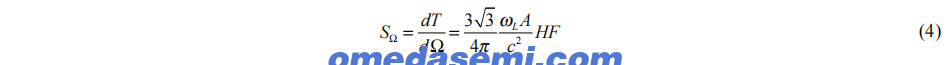
其中F是谐振器的精度，H是共振深度（当谐振器处于临界耦合状态时，H = 1），A是谐振器所围成的面积。为了实现最大灵敏度，必须选择输入耦合器的耦合比，以最大化H和F的乘积。增加输入耦合增加了共振深度，但也会引入额外的谐振器损失，从而降低了精度。最大化灵敏度的最佳折衷是临界耦合的一半，这使得H等于8/9。

在图3中，预测的ARW（角随机漫步）在对数-对数坐标系中绘制，横坐标为平衡探测器上检测到的总功率Pdet，纵坐标为我们的陀螺仪条件下的ARW，即具有100百万内在Q因子和面积等于5.8毫米半径环的谐振器，激光带宽为10 kHz，RIN为-140 dBc（由Pure Photonics提供的数值）。输入耦合比选择为最大化旋转灵敏度，使得共振深度为88.9%，精度为1890。激光频率噪声与激光带宽的平方根成正比，并乘以传输光谱的斜率。平衡探测器（见图2）抑制了诸如RIN和激光频率噪声等互易噪声源，抑制幅度为25 dB，这是探测器制造商提供的规格。因此，图3中绘制的RIN和激光频率噪声是计算得出的RIN和激光频率噪声，经过25 dB的衰减。探测器噪声是一个常数，与检测到的功率无关，光子噪声与检测到的功率的平方根成正比，而激光频率噪声和RIN都与检测到的功率成正比。该探测器还贡献了0.4 pW/√Hz的探测器噪声，这是经过测量得到的。由于ARW是噪声与信号的比率，因此探测器噪声限制的ARW（红色点划曲线）与1/Pdet成正比，因为探测器噪声与检测到的功率无关，而信号则与检测到的功率线性增加（见方程（3））。类似地，计算得出的光子噪声限制ARW（实心蓝色曲线）具有-1/2的斜率，激光频率噪声（橙色虚线曲线）和RIN（绿色虚线曲线）则是常数。总ARW（实心黑色曲线）是所有这些统计独立噪声源的平方和。对于小的检测功率，ARW受到探测器噪声的限制。增加输入功率可改善ARW，直到激光频率噪声限制被达到并在大功率下占主导地位。即使在大约10 µW的小检测功率下，ARW也不会远高于此激光频率噪声最小值。该ARW最小值为7.4 deg/h/√Hz，或0.12 deg/√h。如果能够抑制背向散射噪声，这是当前硬件可以实现的最小ARW。

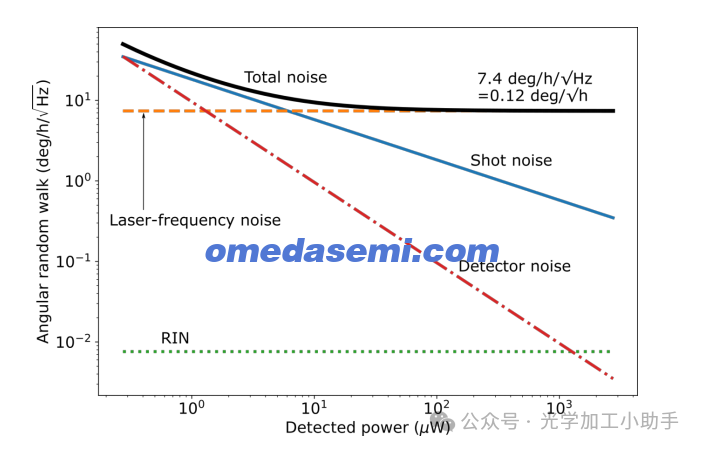
图3. ARW与平衡探测器检测到的总功率的关系图，计算了图2中共振陀螺仪组件的ARW。该模型考虑了探测器噪声、光子噪声、RIN和激光频率噪声。

2.3 SiN谐振器中的背向散射 为了理解环形谐振器中背向散射的一种表现形式，即反向传播信号的耦合，我们使用了[12]中开发的数学模型。感兴趣的量是当光仅以一个方向（例如CW方向）入射时，环形谐振器的传输和反射光谱。环形谐振器中分布式弹性背向散射的存在通过一个功率背向散射系数αB来建模。当前向传播的光在环形谐振器中积累并背向散射到环形波导的反向传播模式时，这种背向散射模式在CCW方向上共振，因为它与CW光具有相同的共振频率。尽管光仅以一个方向（CW方向）入射到环形谐振器中，但两个模式（前向传播和后向传播波）都会被激发。因此，这种背向散射场可能变得很强，并再次向CW方向背向散射，并与CW光场发生干涉。正如在其他耦合模式系统中已知的那样，这种耦合会导致共振频率的分裂，分裂大小与耦合强度成正比，耦合强度与αB有关。因此，通过测量传输光谱中的分裂，可以测量共振频率处的αB。对这种频率分裂的建模最好使用时间耦合模式理论，在这种理论中，前向场和后向场通过耦合速率（以秒的倒数表示）而不是功率耦合系数（以米的倒数表示）相关联。

根据[12]的模型，前向场EFW和后向场EBW通过以下耦合方程描述：

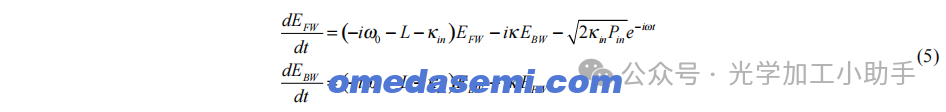
其中，ω是激光频率，Pin是激光调谐到非共振状态时检测到的功率，L = ω/(2Qint)是内在损耗率，其中Qint是谐振器的内在Q因子。在这个描述中，|EFW|²是前向传播模式中储存的能量，|EBW|²是后向传播模式中储存的能量。参数κin = cK/(2Pneff)是输入耦合器的耦合速率，其中K是输入耦合器的功率耦合比，P是赛道的周长。由于背向散射导致的反向传播波之间的功率耦合由κ = c√αB/(neff√P)描述，其中αB是波导在共振频率下的背向散射系数。环形谐振器传输的场ET和反射的场ER是12

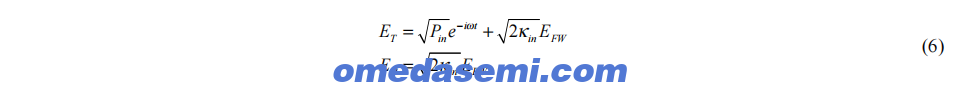
解耦合微分方程（5），并将解代入（6），得到以下功率传输和反射的表达式：

图4绘制了在两个不同的谐振频率下测量的功率传输（蓝色曲线）和反射（橙色曲线）光谱，这两个谐振频率的回散射水平差异很大，图4a中回散射相对较强，图4b中则非常弱。在图4b中，为了提高可见性，反射光谱乘以了一个100倍的因子。当回散射较弱时，回散射会导致谐振在两个方向上轻微的拓宽，这种效应只能通过精密仪器检测到，但肉眼无法看到，正如图4b中的例子。当分裂足够大时，超过大约谐振线宽，谐振会显著分裂，如图4a所示，并且如[12]中所观察到的。

更强的回散射会导致更强的模式耦合，这使得分裂和从环形谐振器反射的功率增加，谐振传输的高度减少（因为功率守恒）。为了量化这种关系，图4a和4b中的传输光谱被拟合到方程（7），以确定每个谐振频率下的回散射系数αB。拟合结果绘制为虚线曲线。进行这些拟合时使用的参数有κin、κ、L和ω0。通过拟合得到的κ值以及已知的环形的周长P和模式折射率neff = 1.52，可以推算出αB的值为：图4a为−66 dB/mm，图4b为−95 dB/mm。然后，将κin、L、κ和ω0插入方程（8）计算每个图中的反射光谱，结果也绘制为虚线曲线。在弱回散射和强回散射情况下，测量和预测的反射光谱之间的吻合度非常好。这一分析确认了图4a中的传输光谱分裂和较强的反射是由于更强的回散射造成的。

为了进一步表征环形谐振器的回散射特性，我们使用商用光学回散射反射仪（OBR）在大约1.5 µm的波长范围内测量了其回散射系数。测量值为−70.5 dB/mm。在此测量中，探针激光的频率在一个广泛的波长范围内扫描，这提供了一个在多个谐振频率上平均得到的αB值。尽管回散射通常在波长上有较弱的依赖性（以数十纳米为尺度），且这种测量通常足以提供一个有意义的αB值，但在这个谐振器中，回散射随波长变化很大，如图4所示，因此仅仅知道平均的αB值并没有太大帮助。通过测量传输光谱并将其拟合到我们的模型中来推导αB是更加优选的方法，因为它更简单，而且如图4所示，非常准确。

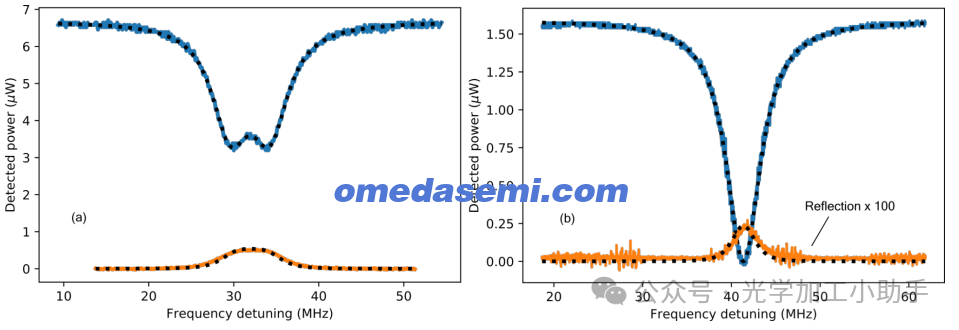
图4. 测量了SiN跑道型谐振器的两种不同谐振频率的传输和反射光谱。传输光谱被拟合到理论模型。传输拟合中的参数用于预测反射光谱。

我们假设这种背向散射的强波长依赖性是由于SiN波导的侧壁或折射率中的偶然周期性扰动，更可能是前者。尽管这些周期可能是随机的，但它们会产生多种具有紧密间隔的布拉格波长和不同强度的光栅。然后，预期会在与布拉格波长重合或靠近更强光栅的布拉格波长的谐振频率上发生更多的背向散射。对SiN环中光栅的初步建模确认，一个在某个谐振频率处非常弱的光栅，其强度恰好能产生约-70 dB/mm的背向散射，将只影响该谐振频率处的背向散射，而不会影响两个相邻谐振频率（它们相隔一个自由光谱范围，即5.45 GHz）。因此，图5中看到的强波长依赖性与SiN波导局部模式指数中的随机周期性变化是一致的。

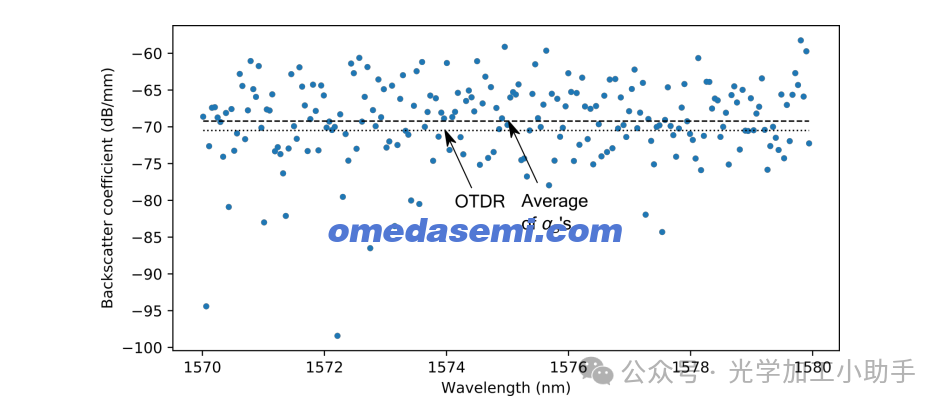
图5. 通过将每个谐振的传输谱拟合到理论模型，测量了200个相邻谐振频率范围内的背向散射系数，覆盖了10纳米的范围。每个蓝点表示在某个谐振频率处测得的背向散射系数。黑色虚线在-69.2 dB/mm处是测量的所有200个谐振频率处背向散射系数的平均值。黑色点线在-70.5 dB/mm处是通过光学背向散射反射计测得的背向散射系数。

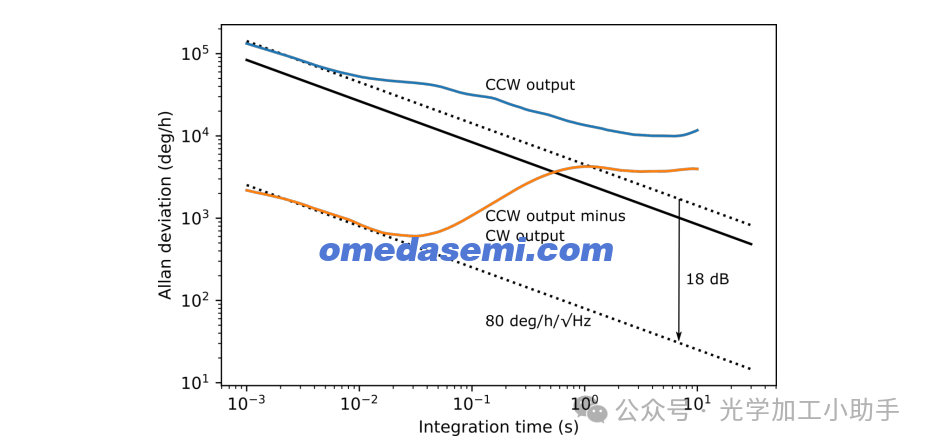
图6. 图2中的陀螺仪的 Allan 偏差测量在最低背向散射谐振点处进行，其中 αB = −98 dB/mm。蓝色曲线是仅测量 CCW 输出的 Allan 偏差。橙色曲线是平衡探测输出的 Allan 偏差，其中从 CCW 输出中减去了 CW 输出。黑色实线曲线是期望的 Allan 偏差，假设在噪声减除之前，ARW 受限于 10-kHz 线宽激光的激光频率噪声。虚线曲线是对这些测量的 Allan 偏差在短积分时间下的拟合。

为了测量背向散射对陀螺仪 ARW 的影响，平衡探测器输出的 Allan 偏差（在减去 CW 和 CCW 信号之后）在四个具有不同背向散射系数的谐振点上进行了重复测量，背向散射系数范围从 −78 dB/mm 到 −95 dB/mm。这些结果如图7所示。在所有积分时间下，随着背向散射系数的降低，Allan 偏差持续减小。这个结果强烈表明噪声受背向散射的限制。

图8绘制了从这四个 Allan 偏差中测得的 ARW 与背向散射系数的关系。如预期，ARW 随着背向散射的增加而恶化。它的斜率约为 0.4，这表明 ARW 与背向散射系数的平方根几乎成正比。这与受背向散射噪声限制的干涉陀螺仪的 ARW 相一致，已知其与背向散射系数的平方根成正比 √αB。13 这种依赖关系表明，这种 SiN 谐振器陀螺仪的限制因素是背向散射噪声。要想在此架构下获得更好的 ARW，需要在此及其他 SiN 芯片中寻找具有更低背向散射系数的谐振点，和/或采用更好的方式来取消背向散射噪声。

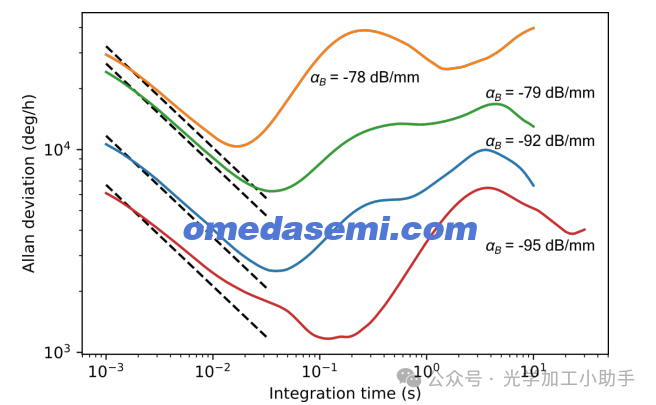
图7. 在四个不同谐振点处进行的 Allan 偏差测量，每个谐振点具有不同的背向散射水平。

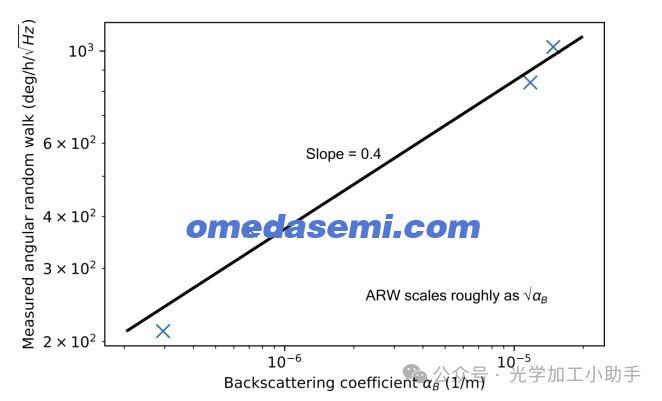
图8. 测量的陀螺仪 ARW，分别在具有不同背向散射系数的谐振点上探测，并绘制与该谐振点的背向散射系数的关系。

3. 总结

本研究展示了一种共振光学陀螺仪，采用了芯片级波导谐振器，形状为跑道，周长为37毫米，内在Q因子为108。该谐振器由超低损耗（0.4 dB/m）的单模SiN波导制成，使用CMOS兼容工艺制造。陀螺仪通过一个10 kHz线宽的半导体激光器探测，并实现了平衡探测方案，成功消除了18 dB的激光频率噪声。环形波导的背向散射水平被发现随着谐振点的不同而变化，变化范围超过四个数量级。研究人员识别出了一个特殊的低背向散射谐振点，其中背向散射系数比使用光学背向散射反射仪测得的平均值（−70.5 dB/mm）小约1000倍（−98 dB/mm）。在这一最低背向散射谐振点上探测，并实施调制方案进一步减少背向散射噪声后，陀螺仪展示出了80 deg/h/√Hz（1.3 deg/√h）的ARW，这在我们所知的情况下，是基于Sagnac效应的芯片级光学陀螺仪在单位面积上的ARW纪录，较此前降低了约2倍。通过在更高背向散射水平下操作陀螺仪，发现ARW大致与√αB成正比，表明噪声受背向散射限制。为了改善陀螺仪的噪声，显然有必要进一步降低背向散射水平，或采取更好的方法来取消背向散射噪声。这样，ARW将受到激光频率噪声的限制，达到16 deg/h/√Hz，并且通过更好的平衡探测和/或更窄的激光线宽，可能会获得更低的值。

结论

本研究展示了一种共振光学陀螺仪，采用了芯片级波导谐振器，形状为跑道，周长为37毫米，内在Q因子为108。该谐振器由超低损耗（0.4 dB/m）的单模SiN波导制成，使用CMOS兼容工艺制造。陀螺仪通过一个10 kHz线宽的半导体激光器探测，并实现了平衡探测方案，成功消除了18 dB的激光频率噪声。环形波导的背向散射水平被发现随着谐振点的不同而变化，变化范围超过四个数量级。研究人员识别出了一个特殊的低背向散射谐振点，其中背向散射系数比使用光学背向散射反射仪测得的平均值（−70.5 dB/mm）小约1000倍（−98 dB/mm）。在这一最低背向散射谐振点上探测，并实施调制方案进一步减少背向散射噪声后，陀螺仪展示出了80 deg/h/√Hz（1.3 deg/√h）的ARW，这在我们所知的情况下，是基于Sagnac效应的芯片级光学陀螺仪在单位面积上的ARW纪录，较此前降低了约2倍。通过在更高背向散射水平下操作陀螺仪，发现ARW大致与√αB成正比，表明噪声受背向散射限制。为了改善陀螺仪的噪声，显然有必要进一步降低背向散射水平，或采取更好的方法来取消背向散射噪声。这样，ARW将受到激光频率噪声的限制，达到16 deg/h/√Hz，并且通过更好的平衡探测和/或更窄的激光线宽，可能会获得更低的值。

作者：Matthew J. Grant*a, Pierre-Baptiste Vignerona, Avi Feshalib, Warren Jinb, Nathan Abramsb,

Mario Panicciab, and Michel Digonneta

单位：a-Edward L. Ginzton Laboratory, Stanford University, 348 Via Pueblo Mall, Stanford, CA, USA;

b-Anello Photonics, Santa Clara, CA, USA